Bilinear

A function f(x,y) is bilinear if the following is true, where m any constant:

  • f(mx,y)=mf(x,y)
  • f(x,my)=mf(x,y)
  • f(x1+x2,y)=f(x1,y) + f(x2,y)
  • f(x,y1+y2)=f(x,y1) + f(x,y2)

Yhis extends what “linear” did for f(x) to a function with two variables. For an example, we test f(x,y) = xy.

  • f(mx,y) = (mx)y = mxy
  • f(x,my) = x(my) = mxy
  • mf(x,y) = m(xy) = mxy
  • f(x1+x2,y) = (x1+x2)y = x1y + x2y
  • f(x1,y) + f(x2,y) = x1y + x2y
  • f(x,y1+y2) = x(y1+y2) = xy1 + xy2
  • f(x,y1) + f(x,y2) = xy1 + xy2

Two 3D graphs have been made to show f(x,y)=xy.

f(x,y)=xy
f(x,y)=xy For this graph, the scaling of the z-axis does not match the scaling for the x-axis and the y-axis.

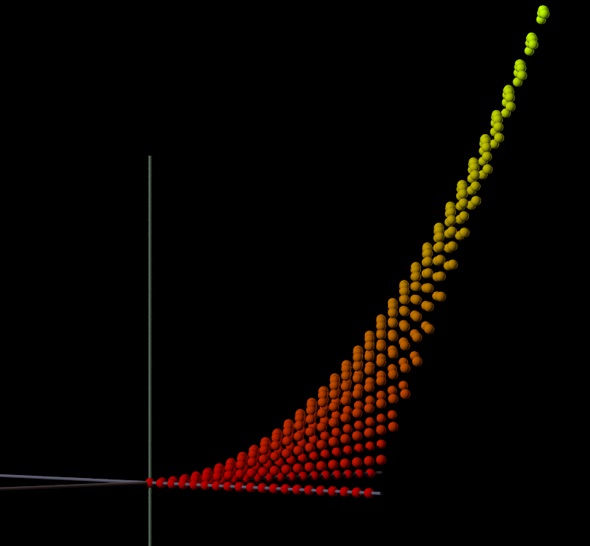
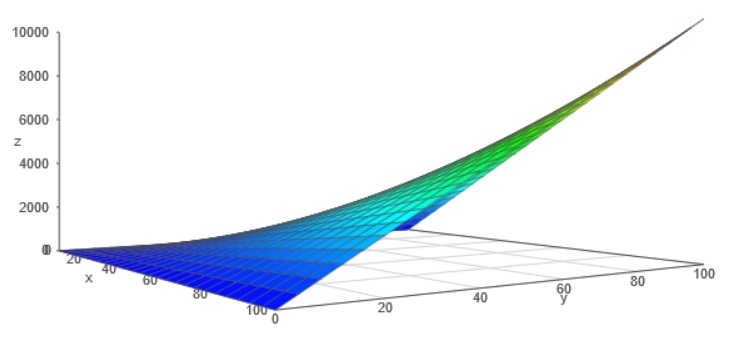
If you take a slice that runs parallel to the x-axis (or the y-axis) you get a function that is linear (example: (2,0,0), (2,1,2), (2,2,4), (2,3,6), (2,4,8), (2,5,10), etc. However, if you “go up the middle” (0,0,0), (1,1,1), (2,2,4), etc. and you can see that the “run” is \sqrt 2) between adjacent point, a constant, but that the rise is Exponential (0,1,4,9,16, etc.).

Appendix A

The Dot Product is bilinear.

  • Let a=(a_1 + a_2 + ... + a_n)
  • Let b=(b_1 + b_2 + ... + b_n)
  • ma \cdot b= (ma_1)b_1 + (ma_2)b_2 + ... + (ma_n)b_n = ma_1b_1 + ma_2b_2 + ... + ma_nb_n
  • a \cdot mb = a_1(mb_1) + a_2(mb_2) + ... + a_n(mb_n) = a_1mb_1 + a_2mb_2 + ... + a_nmb_n = ma_1b_1 + ma_2b_2 + ... + ma_nb_n