Relativity Right Triangle

The goal here is to show the reader, in a manner as simply and quickly as can be done, how to set up a right triangle whose sides can be used to calculate the formula shown below:

$T = \dfrac {T_0}{\sqrt{1 - \dfrac{v^2}{c^2}}}$

We have an experiment that has a starting point and a stopping point. We can’t anchor these points to time, as we normally would do.

The train is moving the x direction at a velocity of v. You shine a light that goes from one side of the train to the other, and this is the y direction.

What comes next may be a bit confusing at first, maybe. Yes, we know the train is moving, but, because we are on the train, our frame of reference moves at the same velocity of the train so, our frame of reference is the stationary frame. It seems to us that we are still, and the ground and the surroundings are moving at velocity v.

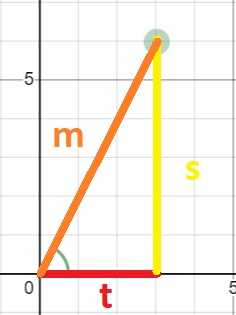
For our perspective, when we shine the light, it only moves in the y direction. This is side s of our right triangle. We turned on the light at the start of the experiment and it reached the other side of the train at the stopping point of the experiment.

Between the start and stop of the experiment the train moved a distance t (t for train). Alternately, the ground moved a distance t and we were still.

From the frame of reference on the ground, the light had to move a distance t in the x direction, and also move a distance s in the y direction, between the start and stop of the experiment. From this we can calculate the distance traveled by the light as would be reported by the person on the ground–we call that distance m.

The distance m is clearly longer than the distance t, yet they traveled at the same velocity (the speed of light). In order for velocities to be equal, unequal distances must correspond to unequal amount of time. A longer distance requires more time.

Because the triangle is a right triangle, we can put the the lengths of the sides of the triangle into the Pythagorean Theorem.

$m^2 = s^2 + t^2$

Recall that velocity is distance traveled per unit time: v = d/t

We can arrange this to distance is velocity multiplied by time: d=vt

Each side of the triangle is a distance and we can convert each d to a vt.

Back to the “weird” for a moment. The perspective of being on the train is the frame of reference we call “stationary”–for this frame there is no movement in the x direction. We will call the time for this, $t_s$ .

The light moves in both the x direction and the y direction when we use the ground frame of reference. We call time for this $t_m$ .

The side t has movement in the x direction because it also has a perspective anchored to the ground, therefore it too uses $t_m$ .

$s=c \: t_s$
$m= c \: t_m$
$t = v \: t_m$

$s^2 + d^2 = m^2$

$c^2 t_s^2 + v^2 t_m^2 = c^2 t_m^2$

We divide each term by $c^2$ :

$t_s^2 + \dfrac {v^2} {c^2} t_m^2 = t_m^2$

$t_s^2 = t_m^2 - \dfrac {v^2} {c^2} t_m^2$

$t_s^2 = t_m^2(1 - \dfrac {v^2} {c^2})$

$\dfrac{t_s^2}{t_m^2} = 1 - \dfrac {v^2} {c^2}$

$\sqrt{\dfrac{t_s^2}{t_m^2}} = \sqrt {1 - \dfrac {v^2} {c^2}}$

$\dfrac{t_s}{t_m} = \sqrt {1 - \dfrac {v^2} {c^2}}$

For some problems, we are done at this point. We’ll do a few more rearrangements though:

$\sqrt {1 - \dfrac {v^2} {c^2}} = \dfrac{t_s}{t_m}$

$t_m = \dfrac{t_s}{\sqrt {1 - \dfrac {v^2} {c^2}}}$

Commentary about extra “free, no charge” things

When you read that more time was needed for the frame of reference on the ground, I’m hoping you thought “A-ha! comparatively speaking there was, thus, less time needed for the frame of reference on the train–and we were expecting that traveling at a high velocity would make clocks slow down.

Because our train must be traveling less than the speed of light, that means the shortest side of the triangle will always be the distance traveled by the train.

The above paragraph constrains the light traveling in the stationary frame of reference to be the longer side of the triangle. Now with both sides taken, only the hypotenuse remains unclaimed.

Light, traveling in the y direction because we aimed it that way, and also in the x-direction because of the trains velocity, must correspond to the hypotenus.

At this point we have accounted for all three sides of the triangle.

Share this: