Tensor is a word that covers Scalars, Vectors, Matrices and higher ranking structures.
It would appear the word is used when the object has a rank higher than matrices, else the object is called a word like scalar, vector or matrix.
- rank 0 tensors – scalars
- rank 1 tensors – vectors
- rank 2 tensors – matrices
A tensor is a container that stores components.
- A vector is a “stack” of scalars
- A matrix is a “stack” of equal sized vectors
- A tensor of rank three is a “stack” of equal sized matrices
Vectors are independent of their frame of reference, but their frame of reference provides the numbers we use to describe the vector. This concept generalizes to all objects that we call tensors. It should make sense that if a tensor collected data in inches for all its components, we could scale that tensor by 2.54 to convert all the numbers to centimeters.
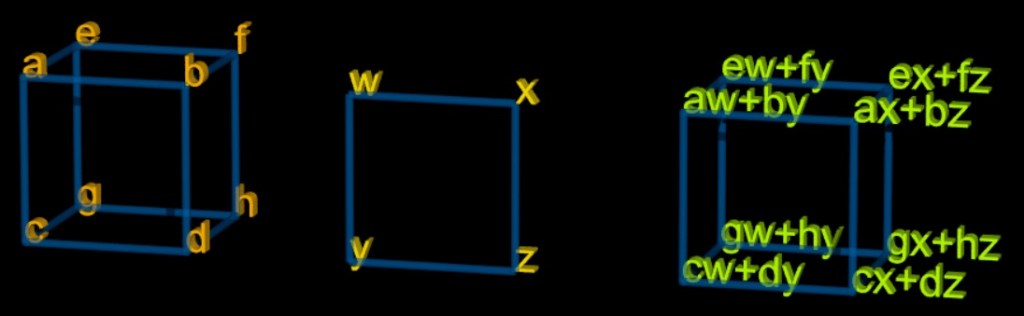
A matrix can be used to convert a vector from one frame of reference to another. There is summation involved in this, but it may be written in a way that we don’t use a summation symbol–rather, we have to know there is a summation involved because of something we see in the notation. The rules is, if you see a variable twice in a math expression, it is involved in a summation. Notice that below, occurs twice.
Assume we are using matrix A to go from v to v’.
Appendix A
The exercise below represents a rank 3 tensor (2×2×2) by showing two side by side (2×2) structures and multiplying this by a (2×2) structure to obtain another rank 3 tensor.