In a way, Trigonometry crashed the party in Geometry when, after we learned about Right Triangles, we learned about the relations of three trigonometric functions: sine, cosine, and tangent.
Sine
The graph below is Sine (theta) as a function of theta, with theta being degrees.

Cosine
The graph below is Cosine (theta) as a function of theta, with theta being degrees.

Reciprocal Trigonometric Functions are introduced. Some caution is needed. Functions like Sine and Cosine are periodic and this means that different angle values will give the same function value. Therefore, the inverse function could go to more than answer (eek! technically it isn’t a function!) so your calculator has a protocol to decide which angle is the “go to” angle for your input. I think values below 90 degrees are “safe” for having Sin^-1(x) take you back to where you started.
Let’s test sin(x) and sin-1(x).
30 degrees in radians is pi/12 which is 0.261799.
- sin(0.261799) = 0.2588186705
- sin^-1(0.258819) = 0.2617993411
Stare at these results for a minute and do the following:
0.261799 = sin^-1(0.258819) so change the first one to:
sin(sin^-1(0.258819)) = 0.2588186705
You can probably see the idea just from looking at that, but we should do one more thing. Regarding variables and values, if a variable is equal to a value we can replace the variable with that value wherever the variable is found–and the opposite is also true:
we can replace a value with the variable, wherever the value is found (Euclid’s Common Notion One). Let x=0.258819 and assume the difference between 0.258819 and 0.2588186705 is round-off error, then we have:
sin(sin^-1(x)) = x
This matches up with the idea of an Inverse Function.
The idea of a Unit Circle shows how points on a circle relate to sine and cosine.
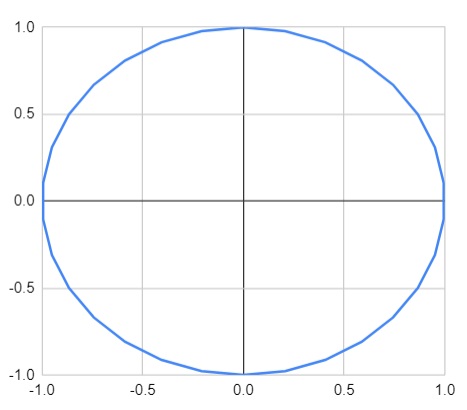
For the measure of Angles, Radians are introduced and compared to Degrees.
Appendix A – Is the Inverse Trigonometric Function really a Function?
Simple answer, no. However, we need it for math sometimes, so they do a trick. If we start at -90 degrees where Sin(-90)=-1 and we stop at 90 degrees where Sin(90)=+1, we don’t have any instance it isn’t one-to-one. When calculating sin-1(x), the computer program takes your input between -1 and +1 and it finds you an angle between -90 deg and +90 deg.
Likewise, for cos^-1(x), the computer takes your input between -1 and +1 and it finds you an angle beween 0 degree and 180 deg. (possible we should tell you that going from -1 to +1 takes you from 180 deg to 0 deg)
.