Unit Circle

$sin^2(\theta) + cos^2(\theta) = 1$

The above is a Trigonometric Identity. Below we have the Pythagorean Theorem with ‘h’ being the hypotenuse and ‘a’ and ‘o’ being the other two sides.

$o^2 + a^2 = h^2$

A right triangle with angle theta, adjacent side ‘a’, opposite side ‘o’ and hypotenuse ‘h’.

Make the following assignments:

1 = h^2
a^2 = cos^2(theta)
o^2 = sin^2(theta)

If h^2 = 1 then h=1 since 1^2=1.

For the next two lines, we take the square root of both sides and get the following:

a= cos(theta)
o= sin(theta)

From this we can construct a graph, with x=cos(theta) and y=sin(theta), or vice versa, and we will get a circle with a radius of 1.

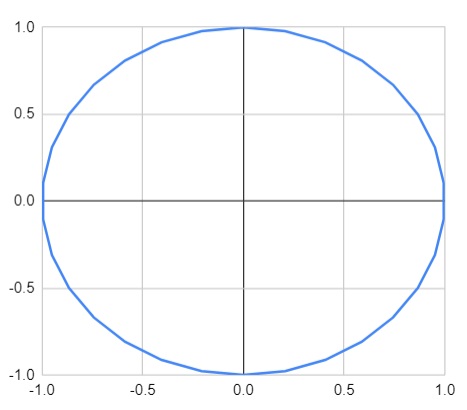
Test this yourself on a spreadsheet. Let build a column for your theta value (caution: your spreadsheet probably requires radians rather than degrees) and then plot two columns, one for sine theta and one for cosine theta, and graph those two columns.

Why does this work? The first equation, $sin^2(\theta) + cos^2(\theta) = 1$ is a guarantee, if you are adding two numbers and the first is sin^2 theta, then, if the second number is cos^2 theta, the sum will be 1.

The above trigonometry identity can be used to construct two more similar trigonometry identities by taking it and first dividing each term by $sin^2(\theta)$ and then dividing each term by $cos^2(\theta)$ :